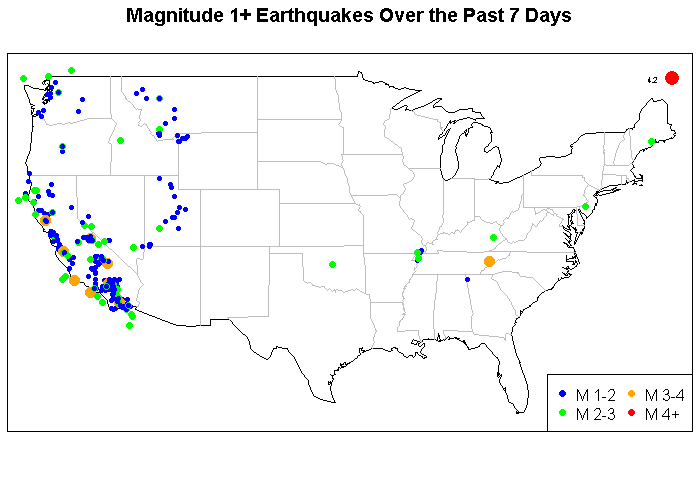
This is a brief example using the maps in R and to highlight a source of data. This is real-time data and it comes from the U.S. Geological Survey. This shows the location of earthquakes with magnitude of at least 1.0 in the lower 48 states.
library(maps)
library(maptools)
library(rgdal)
eq = read.table(file=”http://earthquake.usgs.gov/earthquakes/catalogs/eqs7day-M1.txt”, fill=TRUE, sep=”,”, header=T)
plot.new()
my.map <- map("state", interior = FALSE, plot=F)
x.lim <- my.map$range[1:2]; x.lim[1] <- x.lim[1]-1; x.lim[2] <- x.lim[2]+1;
y.lim <- my.map$range[3:4]; y.lim[1] <- y.lim[1]-1; y.lim[2] <- y.lim[2]+1;
map("state", interior = FALSE, xlim=x.lim, ylim=y.lim)
map("state", boundary = FALSE, col="gray", add = TRUE)
title("Magnitude 1+ Earthquakes Over the Past 7 Days")
eq$mag.size <- NULL
eq$mag.size[eq$Magnitude>=1 & eq$Magnitude<2] <- .75
eq$mag.size[eq$Magnitude>=2 & eq$Magnitude<3] <- 1.0
eq$mag.size[eq$Magnitude>=3 & eq$Magnitude<4] <- 1.5
eq$mag.size[eq$Magnitude>=4] <- 2.0
eq$mag.col <- NULL
eq$mag.col[eq$Magnitude>=1 & eq$Magnitude<2] <- 'blue'
eq$mag.col[eq$Magnitude>=2 & eq$Magnitude<3] <- 'green'
eq$mag.col[eq$Magnitude>=3 & eq$Magnitude<4] <- 'orange'
eq$mag.col[eq$Magnitude>=4] <- 'red'
points(x=eq$Lon,y=eq$Lat,pch=16,cex=eq$mag.size, col=eq$mag.col)
eq$magnitude.text <- eq$Magnitude
eq$magnitude.text[eq$Magnitude<4] <- NA
text(x=eq$Lon,y=eq$Lat,col='black',labels=eq$magnitude.text,adj=c(2.5),cex=0.5)
legend('bottomright',c('M 1-2','M 2-3','M 3-4','M4+'), ncol=2,
pch=16, col=c('blue','green','orange','red'))
box()
[/sourcecode]