The Dirichlet process provides a very interesting approach to understand group assignments and models for clustering effects. Often time we encounter the k-means approach. However, it is necessary to have a fixed number of clusters. Often we encounter situations where we don’t know how many fixed clusters we need. Suppose we’re trying to identify groups of voters. We could use political partisanship (e.g. low/medium/high Democratic vote) but that may not necessary describe the data appropriately. If this is the case then we can turn to Bayesian nonparametrics and the Dirichlet Process and use some approaches there to solve this problem. Three in particular are commonly used as examples: the Chinese Restaurant Model, Pólya’s Urn, and Stick Breaking.
Chinese Restaurant Model
The Chinese Restaurant Model is based on idea that there is a restaurant with an infinite number of tables. At each table there are an infinite number of seats. The first customer arrives and sits down at a table. The second customer then arrives and selects a table. However, the customer selects the table that the first customer is currently sitting with probability or selects a new table with
. This continues on to the
customer where they select a table that a current customer is sitting with probability
.
crp = function(num.customers, alpha) {
table < - c(1)
next.table <- 2
for (i in 1:num.customers) {
if (runif(1,0,1) < alpha / (alpha + i)) {
# Add a new ball color.
table <- c(table, next.table)
next.table <- next.table+1
} else {
# Pick out a ball from the urn, and add back a
# ball of the same color.
select.table <- table[sample(1:length(table), 1)]
table <- c(table, select.table)
}
}
table
}
crp(100, 4)
plot(
table( crp(10000, 2) )
,xlab="Table Index", ylab="Frequency"
)
[/code]
<p style="text-align: center;"><a href="http://statistical-research.com/wp-content/uploads/2013/03/StickBreakingProb.png"> </a>
<h2>Pólya's Urn Model</h2>
In the Pólya's Urn model we take the approach where there exists a urn of colored balls. We take a ball out of the urn and note its color. We replace the ball back into the urn and then we add an additional ball of the same color to the urn. This process can continue on infinitely.
rgb2hex < - function(x){
hex.part = ""
hex <- ""
for(i in 1:3){
b16 <- x[,i]/16
int.one <- trunc(b16)
if(int.one>=10){
val.one < - letters[int.one-10+1]
} else {
val.one <- int.one
}
fract <- abs( b16 - int.one )
int.two <- fract*16
if(int.two>=10){
val.two < - letters[int.two-10+1]
} else {
val.two <- int.two
}
hex.part[i] <- paste(val.one,val.two, sep="")
hex <- paste(hex,hex.part[i], sep="")
}
hex
}
polyaUrnModel = function(baseColorDistribution, num.balls, alpha) {
balls < - c()
for (i in 1:num.balls) {
if (runif(1,0,1) < alpha / (alpha + length(balls))) {
# Add a new ball color.
library(colorspace)
color.comb < - expand.grid(x=seq(0,255),y=seq(0,255),z=seq(0,255))
location.picker <- rnorm(1,nrow(color.comb)/2, (nrow(color.comb)-1)/4 )
the.color <- c( color.comb[location.picker,1], color.comb[location.picker,2], color.comb[location.picker,3])
the.hex <- paste("#",rgb2hex(the.color), sep="")
new.color <- the.hex
balls = c(balls, new.color)
} else {
# Pick out a ball from the urn, and add back a
# ball of the same color.
ball = balls[sample(1:length(balls), 1)]
balls = c(balls, ball)
}
}
balls
}
pum < - polyaUrnModel(function() rnorm(1,0,1), 100, 1)
barplot( table(pum), col=names(table(pum)), pch=10 )
[/code]
<p style="text-align: center;"><a href="http://statistical-research.com/wp-content/uploads/2013/03/BarplotPolyaUrn.png"><img class="aligncenter wp-image-1245" alt="Polya Urn Model" src="http://statistical-research.com/wp-content/uploads/2013/03/BarplotPolyaUrn.png" width="419" height="321" /></a>
<h2>Stick Breaking Model</h2>
<p style="text-align: left;">With this third model we simply start breaking a stick and continue to break that stick into smaller pieces. This process works by taking a stick of length 1.0. We then generate one random number from the Beta distribution ( ~ Beta(1,
~ Beta(1,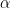 ). We then break the stick at
). We then break the stick at 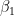 . The left side of the stick we'll call
. The left side of the stick we'll call  . We then take the remaining stick to the right and break it again at location (
. We then take the remaining stick to the right and break it again at location (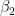 ~<code> </code>Beta(1,
~<code> </code>Beta(1, 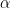 ). Once again the piece to the left we'll call
). Once again the piece to the left we'll call 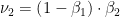 . The sum of all of the probabilities generated will add up to 1.0.</p>
stickBreakingModel = function(num.vals, alpha) {
betas = rbeta(num.vals, 1, alpha)
stick.to.right = c(1, cumprod(1 - betas))[1:num.vals]
weights = stick.to.right * betas
weights
}
plot( stickBreakingModel(100,5), pch=16, cex=.5 )
. The sum of all of the probabilities generated will add up to 1.0.</p>
stickBreakingModel = function(num.vals, alpha) {
betas = rbeta(num.vals, 1, alpha)
stick.to.right = c(1, cumprod(1 - betas))[1:num.vals]
weights = stick.to.right * betas
weights
}
plot( stickBreakingModel(100,5), pch=16, cex=.5 )
Multivariate Clustering
##
# Generate some fake data with some uniform random means
##
generateFakeData < - function( num.vars=3, n=100, num.clusters=5, seed=NULL ) {
if(is.null(seed)){
set.seed(runif(1,0,100))
} else {
set.seed(seed)
}
data <- data.frame(matrix(NA, nrow=n, ncol=num.vars+1))
mu <- NULL
for(m in 1:num.vars){
mu <- cbind(mu,rnorm(num.clusters, runif(1,-10,15), 5))
}
for (i in 1:n) {
cluster <- sample(1:num.clusters, 1)
data[i, 1] <- cluster
for(j in 1:num.vars){
data[i, j+1] <- rnorm(1, mu[cluster,j], 1)
}
}
data$X1 <- factor(data$X1)
var.names <- paste("VAR",seq(1,ncol(data)-1), sep="")
names(data) <- c("cluster",var.names)
return(data)
}
##
# Set up a procedure to calculate the cluster means using squared distance
##
dirichletClusters <- function(orig.data, disp.param = NULL, max.iter = 100, tolerance = .001)
{
n <- nrow( orig.data )
data <- as.matrix( orig.data )
pick.clusters <- rep(1, n)
k <- 1
mu <- matrix( apply(data,2,mean), nrow=1, ncol=ncol(data) )
is.converged <- FALSE
iteration <- 0
ss.old <- Inf
ss.curr <- Inf
while ( !is.converged & iteration < max.iter ) { # Iterate until convergence
iteration <- iteration + 1
for( i in 1:n ) { # Iterate over each observation and measure the distance each observation' from its mean center's squared distance from its mean
distances <- rep(NA, k)
for( j in 1:k ){
distances[j] <- sum( (data[i, ] - mu[j, ])^2 ) # Distance formula.
}
if( min(distances) > disp.param ) { # If the dispersion parameter is still less than the minimum distance then create a new cluster
k < - k + 1
pick.clusters[i] <- k
mu <- rbind(mu, data[i, ])
} else {
pick.clusters[i] <- which(distances == min(distances))
}
}
##
# Calculate new cluster means
##
for( j in 1:k ) {
if( length(pick.clusters == j) > 0 ) {
mu[j, ] < - apply(subset(data,pick.clusters == j), 2, mean)
}
}
##
# Test for convergence
##
ss.curr <- 0
for( i in 1:n ) {
ss.curr <- ss.curr +
sum( (data[i, ] - mu[pick.clusters[i], ])^2 )
}
ss.diff <- ss.old - ss.curr
ss.old <- ss.curr
if( !is.nan( ss.diff ) & ss.diff < tolerance ) {
is.converged <- TRUE
}
}
centers <- data.frame(mu)
ret.val <- list("centers" = centers, "cluster" = factor(pick.clusters),
"k" = k, "iterations" = iteration)
return(ret.val)
}
create.num.vars <- 3
orig.data <- generateFakeData(create.num.vars, num.clusters=3, n=1000, seed=123)
dp.update <- dirichletClusters(orig.data[,2:create.num.vars+1], disp.param=25)
ggplot(orig.data, aes(x = VAR1, y = VAR3, color = cluster)) + geom_point()
[/code]

In this example I have provided some R code that clusters variables based an any given number of variables. The measure of distance from the group centroid is the multivariate sum of squared distance, though there are many other distance metrics that could be implemented (e.g. manhattan, euclidean, etc.)



Dirichlet Process, Infinite Mixture Models, and Clustering http://t.co/K6oaMaqYiy
Dirichlet Process, Infinite Mixture Models, and Clustering http://t.co/FwLEZxi0S6 #mocpekny
“Dirichlet Process, Infinite Mixture Models, and Clustering | Statistical Research” http://t.co/7LQlcHoGTR
Hi there,
Thanks for an interesting post. FYI. The generateFakeData function in your clustering code appears misspecified.
Regards,
Nick
Thanks. WordPress does a weird thing where it puts a space between the < and the - on the Web interface. I fixed that function. It's not my coding style but recently using an = to avoid that very problem when assigning variables.
Hi,
You said that we can use these models when we don’t know the number of clusters we need. However, it seems like they all have an adjustable, user-specified parameter alpha, for which different values would lead to different numbers of clusters. Therefore, by specifying this parameter, you are implicitly setting the number of clusters. Is that the case, or am I missing something?
Thanks,
Matthew
A dispersion parameter is certainly related to the way clusters are created. However, rather than defining the number of clusters in advance the data drives how many clusters are created. In others words once a prior, dispersion parameter, is established if one replicates the study and collects a new batch of data there may very well be a different number of clusters using the same dispersion parameter. Further, the same dispersion parameter on one dataset will likely produce a different number of clusters on another dataset. The dispersion parameter is chosen because it’s some prior piece of information that is known about the data and its clustering. But if you keep on adjusting the prior dispersion parameter then you’re applying a non-informative prior piece of information to effectively obtain the same number of clusters then it’s almost like doing a round-about k-means clustering.
R code shown in the second model, Polya’s Urn Model, rgb2hex function script at line 5, the script may be modified as
b16 <- x[i]/16
instead of
b16 <- x[,i]/16 to avoid the error, Error in x[, i] : incorrect number of dimensions
You can often torture data into confessing anything you want. However, when you set the dispersion parameter a priori you let the data drive the outcome.
Many thanks, especially for the Multivariate Clustering code.
This is the first time I see DP clustering in action and it’s actually really simple!
One question: you are using a distance measure. That is not very probabilistic, is it?
In other words, I would have expected a probability in line 058.
E.g. p(data[i,] | subset(data,pick.clusters == j) ) (excuse my pseudocode… 😉 ).
That’s possible as well right?
You can plug in anything you want, I guess.
Thanks for the write-up, however I don’t think Multivariate Clustering code is a DP ! It doesn’t seem you have chose the Chinese restaurant process.
when i was running chinese restaurant process code in r, i got an error. can u solve my problem
crp(100, 4)
Error in table < -c(1) :
comparison (3) is possible only for atomic and list types
I don’t know if you still update or check this site, but I was trying to implement your multivariate clustering to understand Dirichlet processes better and I don’t quite understand what your code is doing.
No matter what input parameters I give the dirichletClusters function you have written, it ALWAYS finds only a single cluster. In fact, your ggplot code that you provide is only plotting the original data and pre-assigned clusters, not the results of your clustering function at all! So I don’t understand what that clustering function is actually doing, since you don’t present any of the results from it, and when I run it in R it only ever returns 1 cluster.
Hello, Wesley, I am studying your code for Polya’s Urn Model, but I get a weird error at line 5: b16 = x[,i]/16 it says: “Error in x[, i] : número incorreto de dimensões”
BTW: número incorreto de dimensões = incorrect number of dimensions.
Any hint?
So unless I am grossly misunderstanding the purpose here with the Multivariate Clustering, it would appear that in this line of code:
ggplot(orig.data, aes(x = VAR1, y = VAR3, color = cluster)) + geom_point()
You are actually plotting the cluster name (color = cluster) that was output from the generateFakeData function. If instead we plot the cluster assignment reported from the dirichletClusters function, something like:
plot <- data.frame(orig.data, dirichletClusters=dp.update[['cluster']])
ggplot(plot, aes(x = VAR1, y = VAR3, color = dirichletClusters)) + geom_point()
Then the resulting cluster assignments are not 3, as would be expected but instead are 5.